find critical points of multivariate function

Problem

Assume the function $z=f$ is defined in terms of $x$ and $y$, i.e. $z=f(x,y)$. Find the critical points (any minimum, maximum, or saddle point).

At critical points, $f_x=0$ and $f_y=0$, where $f_{(\cdot )}$ is the partial derivative with respect to the corresponding variable. Solve the system of equations for $x$ and $y$. Check the coordinates for extraneous solutions (not sure if this can happen but it might).

second derivative test

For a univariate function $f(x)$, a second derivative test tells:

• if $f(x)$ is concave up (if $f^{\prime \prime }>0$)
• if $f(x)$ is concave down (if $f^{\prime \prime }<0$)
• where inflection points are (where concavity changes)

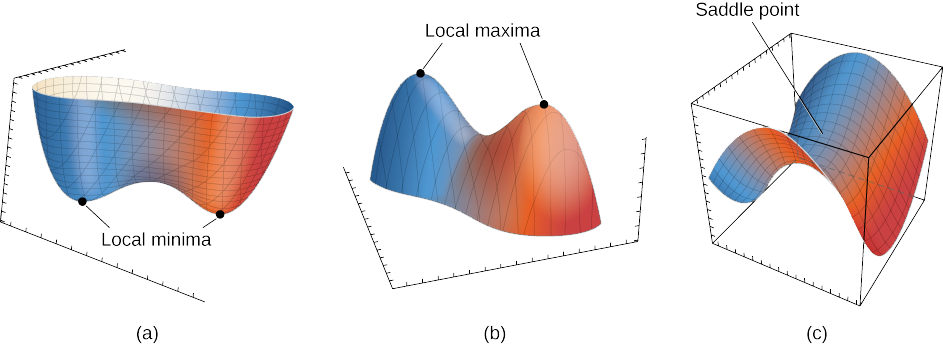
If $f$ is a multivariate function, to determine whether $z=f(x,y)$ has a minimum, maximum, or saddle point at the critical point $P=(x_0,y_0)$, we can use the second derivative test.

First find $f_{xx}$, $f_{yy}$, and $f_{xy}$ ($f_{xx}=\frac{{\partial }^{2}z}{\partial x^2}$, $f_{xy}=\frac{{\partial }^{2}f}{\partial y^2}$, $f_{xy}=\frac{{\partial }^{2}f}{\partial x\partial y}$). Then calculate the determinant $D$ as below:

$$D=f_{xx}(x_0,y_0)\cdot f_{yy}(x_0,y_0)-(f_{xy}(x_0,y_0){)}^2$$

Then:

1. If $D>0$ and $f_{xx}(x_0,y_0)>0$, then $f$ has a local minimum at $P$.
2. If $D>0$ and $f_{xx}(x_0,y_0)<0$, then $f$ has a local maximum at $P$.
3. If $D<0$, then $f$ has saddle point at $P$.
4. If $D=0$ then test is inconclusive.

Link to original