Markov chain

A Markov chain is a memory-less random process. The process is memory-less in the sense that all states have the Markov property.

Mathematically, a Markov chain can be represented by a tuple $⟨\mathcal{S},\mathcal{P}⟩$ where:

• $\mathcal{S}$ is the state space
• $\mathcal{P}$ is the transition probability function (likelihood of state transition given a current state)

We can denote the probability of a state transition $s\to s^{\prime }$ as ${\mathcal{P}}_{s{s}^{\prime }}=\mathbb{P}\left[S_{t+1}=s^{\prime }|S_t=s\right]$ — the transition probability is the chance the the next state is $s^{\prime }$ given the current state at time $t$ is $s$.

We can represent the transition probability function as a matrix. The row number is the source state, and the column number is the destination state. A row $i$ represents how likely a state $i$ can transition to some other state $j$; thus, the probabilities in a single row should sum to one. A sink in the Markov chain has ${\mathcal{P}}_{ss}=1$, meaning that the state can only transition to itself and not any other state.

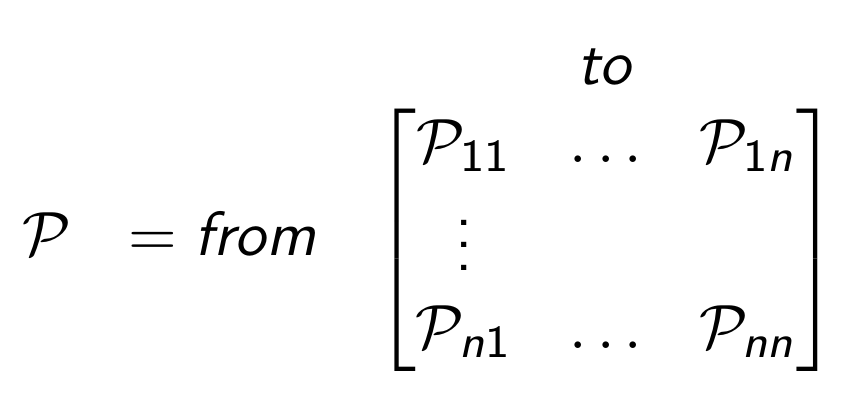
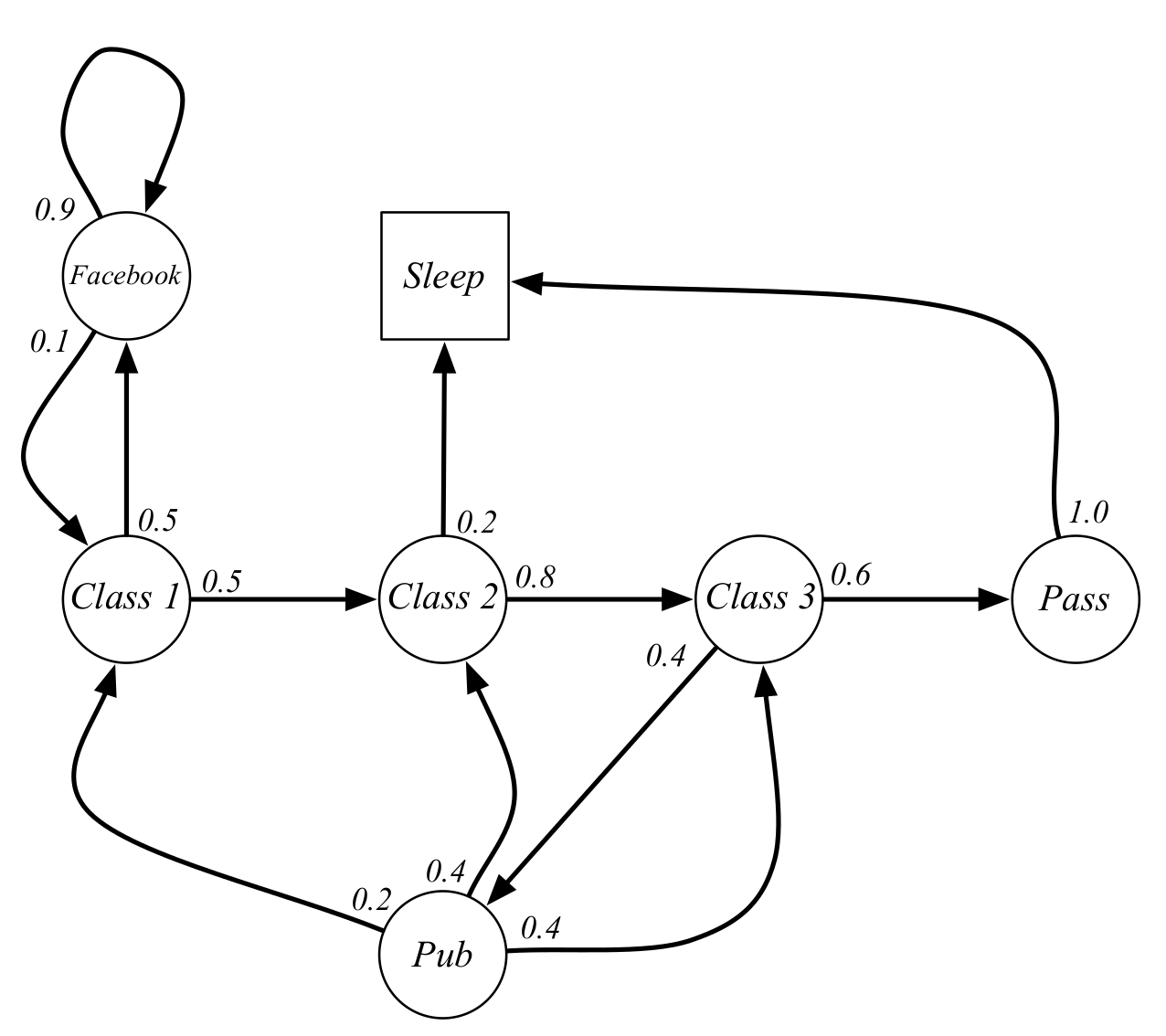
For instance, a college student’s Markov Chain would look like this:

The same Markov chain but with state transition represented as a matrix: