proof by induction

To prove a predicate $P(n)$ by induction, we need to first prove a base case ($P(n_0)$), then demonstrate that if $P(n)$ holds for an arbitrary but fixed $n\ge 0$ then $P(n+1)$ holds as well. This proves $P(n)$ for all $n\ge n_0$ (by the Induction Principle) since $P(n_0)⟹P(n_0+1)$, $P(n_0+1)⟹P(n_0+2)$, etc.

Proof Structure

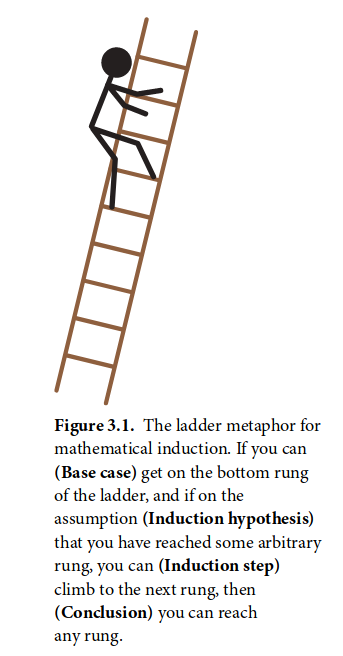
Think of an induction proof as a ladder. We need to step on the first rung and learn how to climb to the next rung. Once we’ve done that, we’re golden for the rest of the ladder, which may as well be infinite. @lewisEssentialDiscreteMathematics2019 Figure 3.1:

Predicate

The predicate is the statement we want to prove stated in terms of the induction variable (which is $n$ most of the times)

Induction Variable

The variable on which we do induction later. Choosing the right value as the induction variable is crucial to the success of the proof — the value should increment for each subsequent case of the predicate.

Base Case

For the base case, we need to prove that $P(n)$ is true for a minimum value $n=n_0$. In other words, prove $P(n_0)$. This part should be trivial for easy proofs as it will just be plugging $n_0$ into an equation or just thinking the statement represented by $P(n_0)$ through. This is equivalent to getting on the ladder (first rung).

Induction Hypothesis

For the induction hypothesis, we simply assume that $P(n)$ is true for any $n\ge n_0$. In terms of the ladder metaphor, this is equivalent to asserting that we have climbed $n$ ladder rungs. Now we only need to prove that we can climb to the $n+1$-th rung in order to show that we can climb the rest of the ladder, too. This step can usually be omitted and is implicit in an induction proof.

Induction Step

In the induction step we must prove that $P(n)⟹P(n+1)$ for an arbitrary but fixed $n$. This is the core of an induction proof and should be the hardest, but once we’ve proven this, we would have effective proven that $\forall n\ge n_0:P(n)$ since the implication we proved works on all $n\ge n_0$, and $P(n_0)$ implies all the rest of the cases by transitivity.

Proof Template

Let $P(n)$ denote… (state what you are trying to prove in terms of $n$)

Proof by induction: $n_0=0$ (change as fit). We need to prove $P(n_0)$: … (show that the base case stands)

(Optional: induction hypothesis) Assume that $P(n)$ is true for an arbitrary $n\ge n_0$.

We now must prove that $P(n+1)$ holds given $P(n)$. … (prove the induction step)

QED.