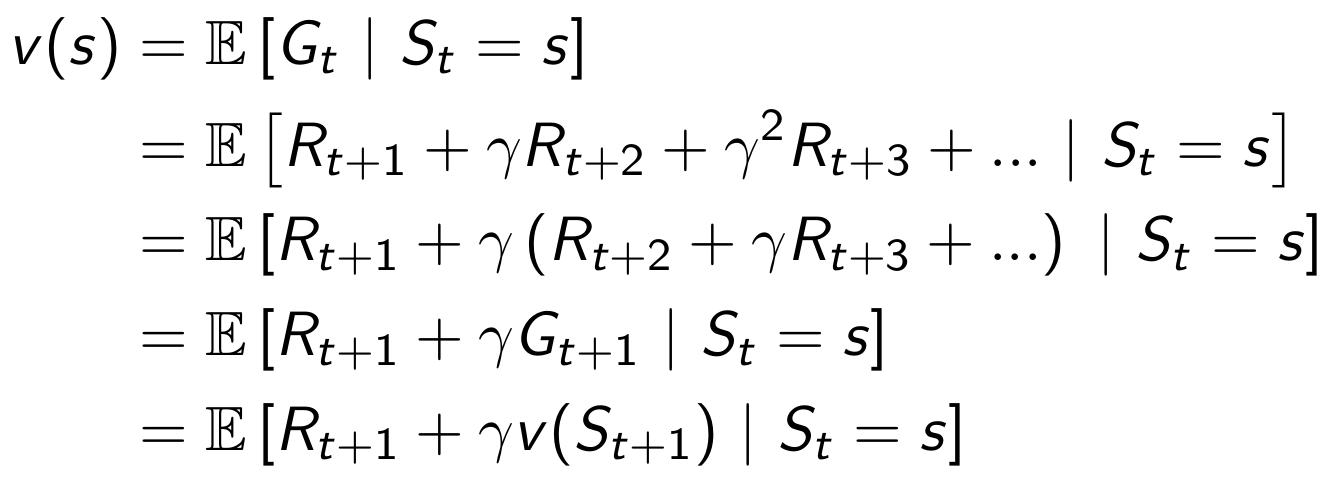Bellman optimality equation for MRP state value

The Bellman optimality equation provides a way to calculate a MRP’s optimal state-value function:

$v(s)={\mathcal{R}}_s+\gamma {\sum }_{s^{\prime }\in \mathcal{S}}{\mathcal{P}}_{s{s}^{\prime }}v\left(s^{\prime }\right)$

The value function works by doing a one-step look-ahead: we are given a recursive formula to calculate $v(s)$ based on $v(s^{\prime })$. The state value is the reward of current state plus the discounted and transition probability-weighted values of the next states (which we need to calculate in advance). Since we need to know the values of the next states, the calculation of the state value function must start at the final states (where it’s just $v(s)={\mathcal{R}}_s$) and propagate the discounted final reward to the initial states.

In matrix form, the state-value function can be represented as: $v=\mathcal{R}+\gamma \mathcal{P}v$

$$\left[\begin{array}{c}v(1)\\ ⋮\\ v(n)\end{array}\right]=\left[\begin{array}{c}{\mathcal{R}}_1\\ ⋮\\ {\mathcal{R}}_n\end{array}\right]+\gamma \left[\begin{array}{ccc}{\mathcal{P}}_{11}& \dots & {\mathcal{P}}_{1n}\\ ⋮& & \\ {\mathcal{P}}_{n1}& \dots & {\mathcal{P}}_{nn}\end{array}\right]\left[\begin{array}{c}v(1)\\ ⋮\\ v(n)\end{array}\right]$$

To actually solve for the value function, we need to get a closed form formula by removing recursion :

$$\begin{array}{rl}v& =\mathcal{R}+\gamma \mathcal{P}v\\ (I-\gamma \mathcal{P})v& =\mathcal{R}\\ v& =(I-\gamma \mathcal{P}{)}^{-1}\mathcal{R}\end{array}$$

Heavy computation

The time complexity of the calculation is $O(n^3)$, so this method is not very practical for large MRPs.

Derivation of equation

The equation can be derived by first decomposing $G_t$ into $\mathbb{E}\left[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}\cdots \right]$. We can recursively calculate the values $R_{s+1}+\cdots$ by replacing the tail of the sum by the second term of the Bellman optimality equation.