recursion tree

A recursion tree visualizes the how a recurrence’s complexity is decreased for subproblems (see divide and conquer).

For the example, if the recurrence is

$$T(n)=T\left(\frac{n}{3}\right)+T\left(\frac{2n}{3}\right)+n$$

then we can build a recurrence tree like below, where each node represents the amount of work done at that node (in this case it’s $n$, which is the subproblem size):

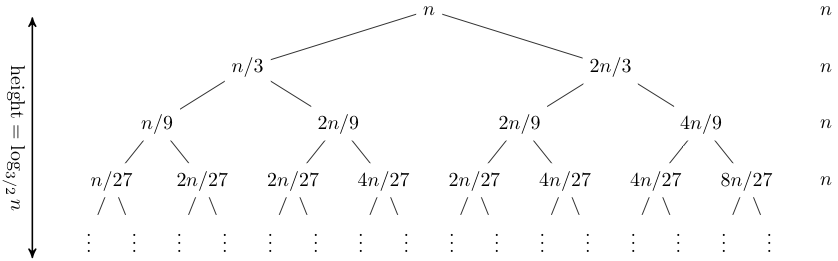
Note that the tree generally stops growing when all subproblems have $n=1$; this determines the height of the tree. For a simple case of $T(n)=a\cdot T\left(\frac{n}{b}\right)+f(n)$, the tree height is ${\log }_{b}n$. For more complex cases like the above, choose the largest $b$ in calculation.

With the recursion tree, we can sum across the row to obtain the number of primitive operations done at each level. We can turn it into a sequence, e.g. $n+n+n+\dots$ for the example above. Use the tree height (i.e. number of terms in the sequence) to obtain a sum, which is the closed-form expression for $T(n)$. So, having ${\log }_{\frac{3}{2}}n$ layers of $n$, the above example yields $T(n)=n{\log }_{\frac{3}{2}}n=O(n\log n)$.

Example

$$T(n)=9T\left(\frac{n}{3}\right)+n^2$$

Now we can create a recursion tree (you can just visualize it since I didn’t want to make a diagram). Excluding the parent problem (work = $n^2$) we have:

Subproblem Layer	Work done at layer
1	$9\cdot {\left(\frac{n}{3}\right)}^2=n^2$
2	$9^2\cdot {\left(\frac{n}{3^2}\right)}^2=n^2$
$i$	$9^i\cdot {\left(\frac{n}{3^i}\right)}^2=n^2$

Now we know the work done at each layer is $n^2$, we can multiply that by the number of layers ${\log }_{3}n$ (tree height) to get:

$$T(n)=O(n^2\log n)$$

The log base of 3 can be ignored since it’s essentially a constant factor.