A pseudorandom permutation (PRP) is a (keyed) bijection from plaintext to ciphertext in such a way that it is not practical to distinguish it from random permutation.
The intuition for why it’s called a permutation is as follows:
Consider a sample encryption permutation for a 4-bit block, which has possible blocks / nodes, each node designated with a hexadecimal digit.
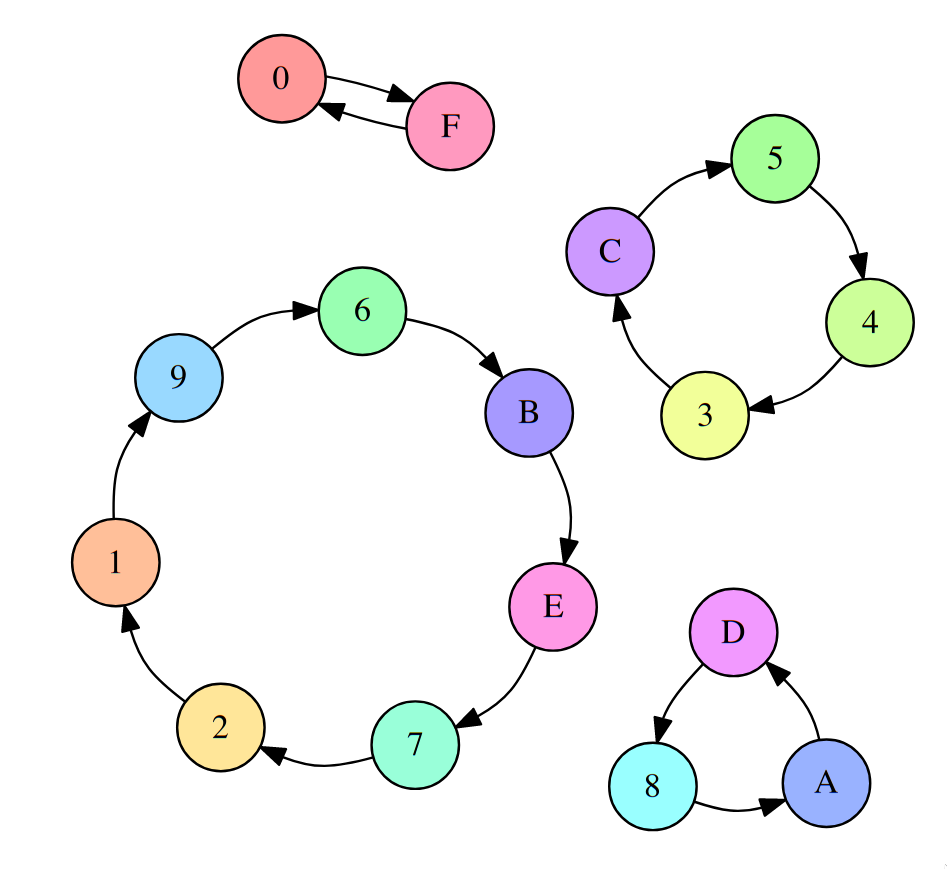(Image from Crypto 101)
Imagine the encryption is implemented with an array containing all possible nodes in order (so array[i] = i). Forget about the need for keys for now. We start by randomly shuffling this array. To encrypt, we index the array using the plaintext block, which spits out the final ciphertext block. As it has become apparent, the permutation is done on the plaintext (as is the case in a transposition cipher), but rather on this array used to encrypt. More formally, this array represents the random mapping of the set of possible blocks onto itself. Note that there are possible permutations for this array. The possible blocks / nodes increase exponentially with block size in bits (), and the possible number of permutations increase factorially ().