countable set

An infinite set $S$ is “countable” or “countably infinite” if there is a bijection $f:\mathbb{N}\to S$. In other words, elements of the set can be labeled with distinct natural numbers.

A set can be countable even though it might not seem like so. For example, although the set $\mathbb{Z}$ seems to have “twice the size” of $\mathbb{N}$, $\mathbb{Z}$ is still countable: Let $f:\mathbb{N}\to \mathbb{Z}$ be a bijection, such that for any $n\in \mathbb{N}$,

$$\begin{array}{c}f(n)=\{\begin{array}{ll}-n/2& \text{if }n\text{ is even}\\ (n+1)/2& \text{if }n\text{ is odd.}\end{array}\end{array}$$

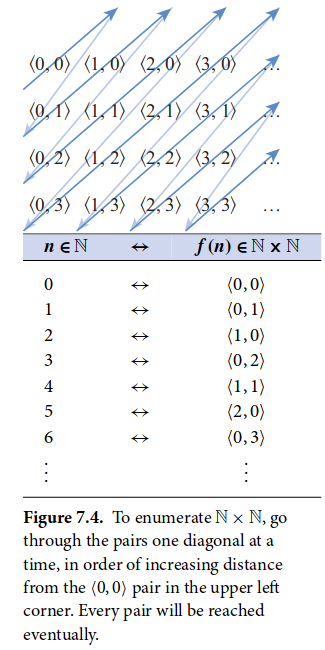
$\mathbb{N}\times \mathbb{N}$ is also countably infinite (see @lewisEssentialDiscreteMathematics2019 Theorem 7.2). Basically we can list these ordered pairs in a certain order and count them with natural numbers.