2023-11-03 lecture 17
find particular solutions in presence of free variables
e.g.
col vec 1, 2, 3 are multiples of each other. 2 free variables?
to find particular solutions, find augmented matrix
and are free variables, so set them to 0 to see that
So this is a solution:
The problem is that how can we define the set of all solutions?
2023-11-05 lecture 18
How can we eliminate a redundant vector ?
The set of vectors are linearly dependent if some produces . Basically if some (if some coefficients are 0) or all vectors can cancel out, the set of vectors are linearly dependent. If all coefficients have to be zero to produce a zero vector, then the set of vectors are linearly independent.
The linearly dependent vector:
(right side doesn’t include )
Columns of a vector are linearly indendent if null space is just the zero vector
2023-11-08 lecture 19
e.g.
Are these vectors linearly independent?
a.k.a. Is the null space of the matrix just zero vector?
We use row operation to delete the third row (two rows are equal) → 3 vectors not linearly independent; one free variable
For we have
which is in the null space
e.g.
Are the columns LI? a.k.a. what’s the nullspace
Since A is a 3 x 4 matrix, we can only have 3 pivots at most! So there is at least 1 free variable. (There can’t be 4 linearly independent vectors in 3D)
2023-11-13 lecture 20
- For a subspace V, dim(V) is the number of vectors in V’s basis.
- Basis vectors allow describing a vector in the vector space as a linear combination of the basis vectors. The coefficients on the basis vectors are the coordinates of in V in terms of those basis vectors.
- Since all vectors in the basis are linearly independent, there is a unique set of coefficients for each vector .
- Proof: Suppose there are two sets of coefficients and . Then
- By the definition of linearly independence, the only solution to this equation is that all coefficient differences are 0 (the trivial solution). Thus .
- Since all vectors in the basis are linearly independent, there is a unique set of coefficients for each vector .
- Pivot columns of A (assume A is in rref) form a basis for . In other words, .
- To show that basis vectors are linearly independent (which is already kind of obvious), show that the only possible linear combination of the basis vector that forms a zero vector is the trivial solution (all zero coefficients).
- To show that the basis vectors span the column space of , simply demonstrate that every column can be rewritten as the linear combination of basis vectors. This should be easy since pivot columns only have an element of 1 in separate row positions.
2023-11-15 lecture 21
- To identify columns of A as basis vectors when A is not in rref, simply turn A into rref and see which columns contain a pivot—the corresponding columns in the original A form a basis/are basis vectors.
- Since we already know that , we know that column’s linear independence (if any) remains the same when A is turned into rref, so we can safely use ‘s pivot columns (LI) to identify basis vectors in A (also LI).
- Generally, , but . In other words, rref does not modify the dimension of the column space.
- To find a basis for
- The special solutions for Ax=0 where A contains free variables form a basis for null(A). Special solutions can be found by setting one free variable to 1 and other free variables to 0.
- Rank nullity theorem: Nullity = number of free variables = number of columns - rank = dim(Null(A))
2023-11-17 lecture 22
- To find the basis for the row space of a matrix
- Row space of A is the column space of A transpose, since they use the same vectors.
- Row space does not change under row operations, so we can use rref to simplify A.
- rref(A) gives us pivot rows. The pivot row vectors, when transposed to column vectors, form a basis for the row space.
- Equivalence
- Note that generally
- e.g.
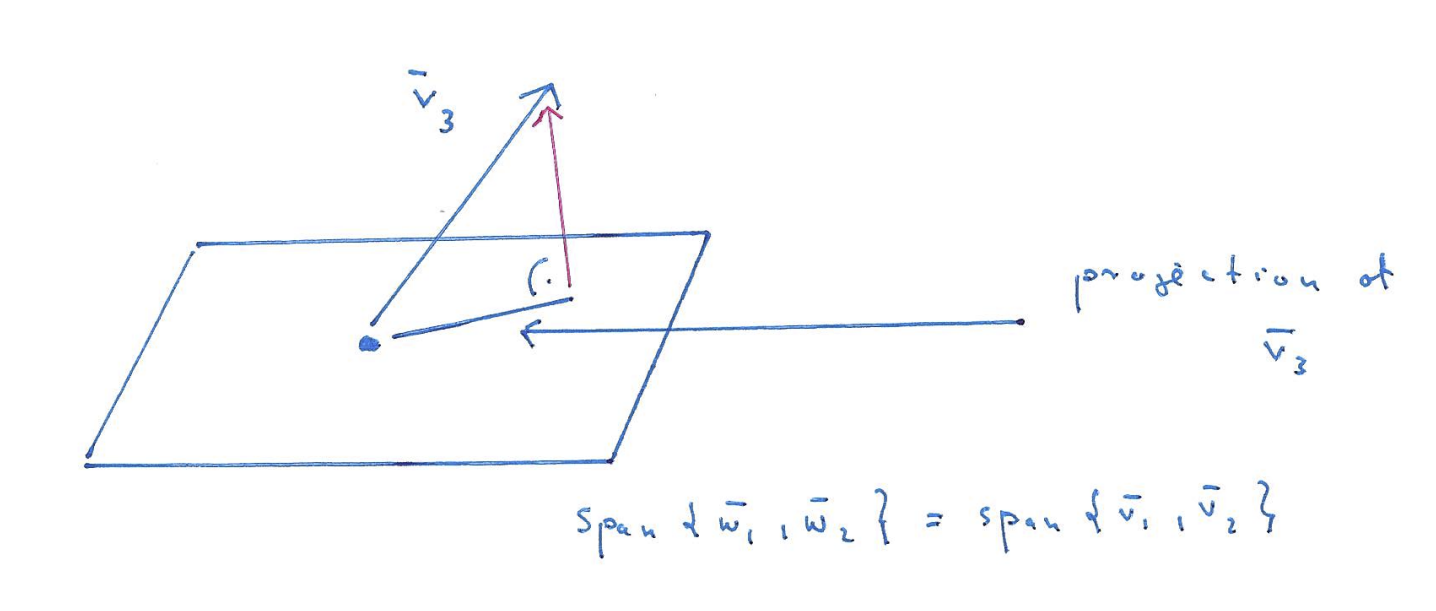
- Projection
- Given a , ( in general).
- Projection of onto is the closest approximation of that still belongs in .
- where is the projection vector and is a vector orthogonal to .
- For each , there is a unique and .
- Say
- It follows that
- Left side is still in , and right side is still a vector orthogonal to , so .
- But since we know both factors are equal, we can rewrite it as , which means . This means that there can only be one . The other factor involving is also zero, so there can only be one .
2023-11-20 lecture 23
- To actually calculate ‘s projection onto , a.k.a. assuming is aline
- Say is a line, so
- . We have to find this
- We know . So .
- , so
- So the projection of onto (given a vector that spans ) is
- If is a unit vector, , so
- To find ‘s projection onto for any matrix
- The projection can be described as for some matrix .
- Condition 1: We know , so we know that for some .
- Condition 2: We know is orthogonal to .
- It follows from condition 2 that , since each row of is a column of , and since all columns of belong to the column space, the dot product of any column with the orthogonal vector will be zero, thus all elements of the product vector will be zero.
- We can get by distributing and then substituting in condition 1.
- When has an inverse, we can use the leftmost and rightmost side to get
- Using the middle side, we get
- So we can use to project any vector onto via .
2023-11-22 lecture 24
- Projection matrix is just an identity matrix without the pivots that are not needed to span .
- Using ‘s definition, we can see that .
- Using the projection matrix method, we can also find the projection of a vector onto a line (spanned by , so ).
- When , is a matrix with a rank of one since we’re projecting onto a line.
- Is ? Yes.
- Generally, -th row of left-hand side is given and are column vectors with rows.
- Generally, -th row of right-hand side is
- Both sides are equal.
2023-11-27 lecture 25
- Projections can be useful for approximating a solution when solution doens’t exist (e.g. estimate line of best fit).
- Solution exists iff
- When solution doesn’t exist, we can find an approximate such that is very close to .
- least squares solution to : To approximate, solve
- Called least squares because the norm of a vector is defined as
- We have
- (solve this equation to get least squares solution)
2023-11-29 lecture 26
- orthonormal basis: basis of a subspace where basis vectors are normal (size 1) and orthogonal to each other.
- Formally, is an orthonormal basis if (orthogonal) and for all (normal).
- Note that orthonormal bases are not unique for a subspace.
- Orthonormal basis is useful for projections.
- If has orthonormal columns, then
- Gram-Schmidt algorithm: makes a basis (e.g. columns of matrix) orthonormal
- Side note: If the basis vectors are already orthogonal, dividing each vector by their norm produces a orthonormal basis.
- Observe that if forms a basis for , then so does .
- This preserves linear independence since when we use the zero vector test, each subtracted term of can be distributed and grouped with the corresponding basis vector . All the coefficients still has to be zero for the linear combination to be the zero vector.
- to be continued
2023-12-01 lecture 27
- Gram-Schmidt algorithm cont’d
- Initial goal: Convert (basis vectors of ) to , where (, i.e. basis vectors are orthogonal). Normality can be achieved easily: divide the orthogonal vectors by norm.
- Say there are 3 basis vectors without loss of generality
- To start, we can make
- To find a orthogonal to , find . Then we can find a vector orthogonal to via .
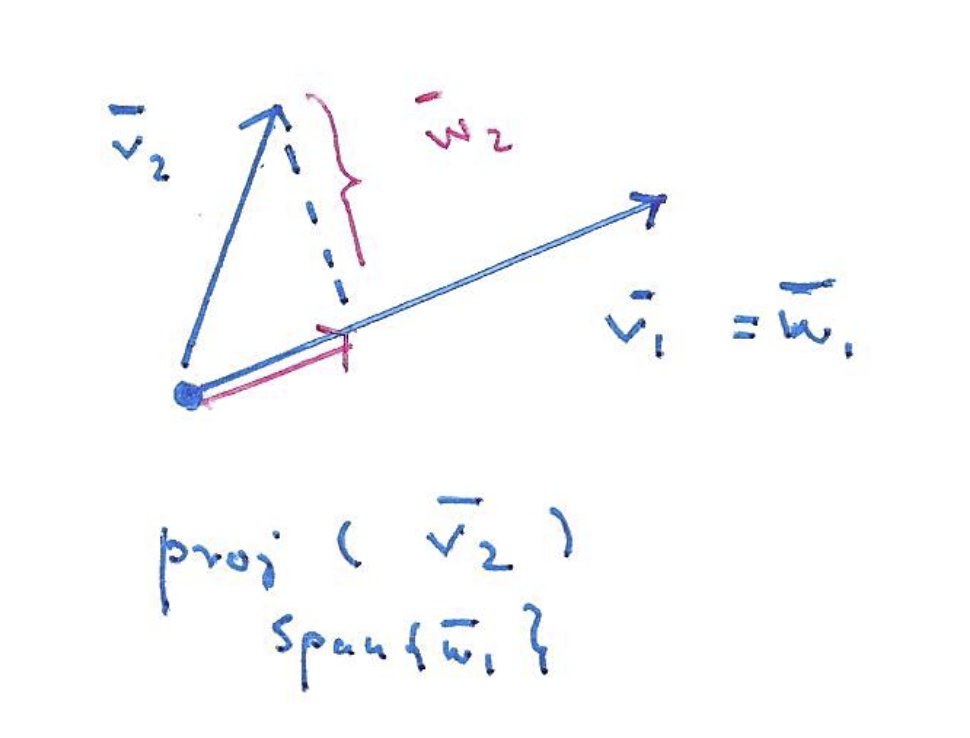
- Note that
- It can also be shown that .
- To find a orthogonal to both and , form a plane with both vectors and subtract the projection of onto the plane from . In other words, . Note that projection onto the plane (with orthogonal basis vectors) can be split into projections onto and like so: .
- If there were more basis vectors , calculate
2023-12-04 lecture 28
- Determinant of a matrix , denoted
- Only square matrices have a determinant.
- If , then is not invertible (i.e. is singular, and is bigger than ).
- where is the identity matrix
- Determinant is the linear function of each row, i.e. if one row was scaled by , then the determinant will also be scaled by .
- Calculating determinant
- If a matrix can be transformed into upper triangular form via row operations (but without switching rows or scaling rows), then where represents the set of diagonal elements.
- If switching rows is needed to transform into upper triangular matrix, then invert the sign of the final determinant. Switching rows an odd number of times also negates the original determinant (switching rows an even number of times does not affect the sign).
- For any 2x2 matrix, .
- If a matrix can be transformed into upper triangular form via row operations (but without switching rows or scaling rows), then where represents the set of diagonal elements.
2023-12-06 lecture 29
- Determinant is primarily a tool to check if is invertible.
- If determinant is non-zero, then we know can be transformed into upper triangular form via row operations.
- Instead of transforming A ourselves, we can calculate directly via the entries of A.
- cofactor expansion
- The cofactor of is the determinant of a smaller matrix where the -th row and -th column of is removed. In addition, the cofactor needs to be negated if is odd. In other words, .
- To calculate , choose a row or column with the most zeros and the greatest elements (this is to make manual calculation easier), iterate over each row or column element , calculate , then sum them together.
- If the cofactor matrix is not 2x2, repeat cofactor expansion recursively.
- Eigenvalue & eigenvector:
- An eigenvector of a square matrix is one such that doesn’t change its direction, but only scales it by , which is called the eigenvalue. Any vector that has the same direction as will also be scaled by the same , and thus is also a eigenvector. There can be multiple eigenvectors with different directions for each . Note that eigenvalues can be negative.
- An eigenvector in a 3D rotation transformation would represent its axis of rotation.
2023-12-08 lecture 30
- Finding eigenvalue & eigenvector
- An easier way to think about solving this equation is to reframe it into , which can be rewritten as . We need to make sure that because we want a non-zero that will only be possible if that matrix is invertible & has a larger nullspace than .
- We can find the set of all eigenvalues by solving , which turns out to be a equation with degree whose variable is .
- To find eigenvectors, solve for the nullspace of for each . Each should result in a nullspace of .
- The formula for Fibonacci numbers can actually be rewritten in linear algebra. . The closed-form formula for Fibonacci sequence actually uses the 2 eigenvalues of .